二端子測定法

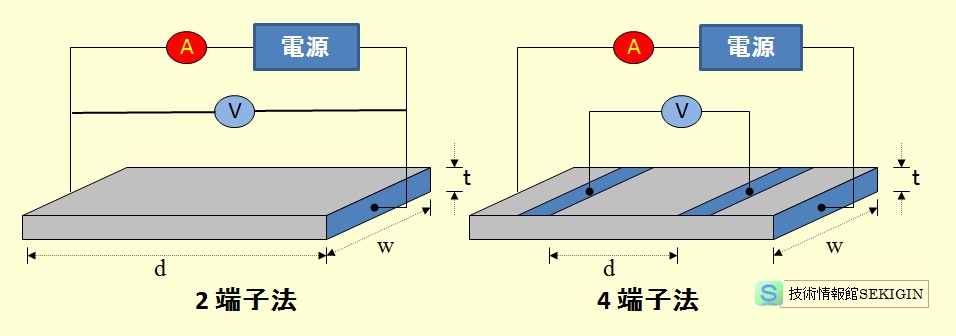
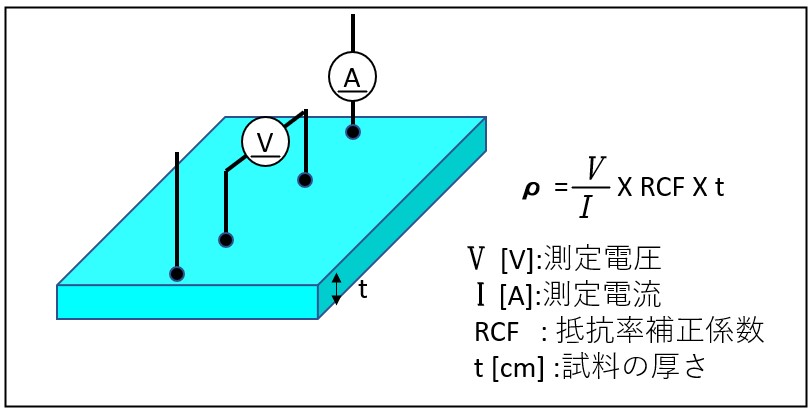
二端子測定法（にたんしそくていほう）は電気抵抗をより正確に測る方法の一つであり、広く用いられているテスター（マルチメータ）での電気抵抗測定に相当する。物性測定において、より高精度であるとされる四端子測定法と比較してこのように呼ばれることがある。

概要

物性測定における二端子測定法は、被測定物の両端に配線を施すだけで測定が可能である一方、接触抵抗および配線自体の抵抗の寄与があるため、測定する抵抗範囲が低い（あるいは超伝導体のように限りなく0に近い）場合には、四端子測定法に比べて測定誤差が大きくなりがちである。測定環境上、四端子測定法を実施できない場合には、測定誤差の寄与を別途評価しこれにより被測定物の結果を補正することで用いられることがある。 接触・配線抵抗と比べて被測定物の抵抗値が十分に高い場合には、配線による熱の流入を軽減するためあえて二端子で測定されることがある。実際に室温~低温用温度センサーなどは半導体が用いられることが多く、低温になるほど抵抗値が高くなるため、二端子測定法で測定されている場合が多い。一般的に、見かけ上温度センサーからは4本の配線が出ているが、センサー部パッケージの中で接続されているため4本ある配線（ V, I,-V,-I）のうち /-だけに気をつければよく、例えば Vと I（あるいは-Vと-I）は同等である。

低温下測定を要する環境以外では、広くテスターとして市販されているように四端子測定法に比べ極めて簡便である。 また、テスターなど、測定レンジ（内部インピーダンス）が選択できる場合、高抵抗用の測定レンジにすることで試料にかかる電流を下げることが出来るため、繊細なデバイスの配線接続のチェックに用いられることもある。

関係式

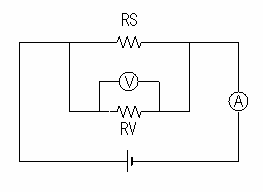
キルヒホッフの電流の法則（図中青矢印）より、

${\displaystyle i=i_{\textrm {S}} i_{\textrm {V}}={\textbf {I}}}$が得られる。

ここで、電源から流れる電流${\displaystyle i}$は、測定される電流値${\displaystyle I}$に等しく、これは被測定物へ流れる${\displaystyle i_{S}}$と電圧計へ流れる${\displaystyle i_{V}}$の和となる。 またキルヒホッフの電圧の法則（図中緑点破線）より

${\displaystyle \left(r_{2} R_{2}\right)\cdot i_{\textrm {S}} R_{\textrm {S}}\cdot i_{\textrm {S}} \left(r_{3} R_{3}\right)\cdot i_{\textrm {S}}=R_{\textrm {V}}\cdot i_{\textrm {V}}}$

および、

${\displaystyle R_{\textrm {V}}\cdot i_{\textrm {V}}={\textbf {V}}}$

を得る。ここで電圧計に流れる電流${\displaystyle i_{V}}$と電圧計の内部インピーダンス${\displaystyle R_{\textrm {V}}}$の積が測定される電圧${\displaystyle {\textbf {V}}}$となる。

測定される電圧・電流の比から電気抵抗を求めると

${\displaystyle {\frac {\textbf {V}}{\textbf {I}}}=\left(r_{2} R_{2} r_{3} R_{3} R_{\textrm {S}}\right)\cdot \left(1-{\frac {i_{\textrm {V}}}{\textbf {I}}}\right)}$${\displaystyle =R_{\textrm {S}} r_{2} R_{2} r_{3} R_{3}-\left(r_{2} R_{2} r_{3} R_{3} R_{\textrm {S}}\right)\cdot {\frac {i_{\textrm {V}}}{\textbf {I}}}}$

となる。第一項が求めたい被測定物の電気抵抗${\displaystyle R_{\textrm {S}}}$であるが、被測定物両端の接触抵抗および配線自体の抵抗、加えて${\displaystyle i_{\textrm {V}}/{\textbf {I}}}$の掛かった項（誤差項）の分だけ本来の値からずれることになる。 ここで、上述の式から誤差項の全電流に対する電圧計へ流れる電流${\displaystyle i_{\textrm {V}}/{\textbf {I}}}$は下のように表すことが出来る。

${\displaystyle {\frac {i_{\textrm {V}}}{\textbf {I}}}={\frac {r_{2} R_{2} r_{3} R_{3} R_{\textrm {S}}}{r_{2} R_{2} r_{3} R_{3} R_{\textrm {S}} R_{\textrm {V}}}}}$

この式から被測定物の抵抗値${\displaystyle R_{\textrm {S}}}$に比較して十分に大きな内部インピーダンス${\displaystyle R_{\textrm {V}}}$をもつ電圧計を用いれば、測定誤差（誤差項の寄与）を小さくすることが出来る 。 四端子測定法に比べると、分子に接触抵抗${\displaystyle r_{i}}$と配線抵抗${\displaystyle R_{i}}$の寄与が入る分、効率は若干低いようである。 定数として足される接触抵抗${\displaystyle r_{i}}$と配線抵抗${\displaystyle R_{i}}$については、金蒸着等により接触抵抗を十分小さくしたり、配線抵抗を参照試料で別途測定・決定し差し引くことで、測定値を補正することが可能である。

脚注

参考文献

日本化学会　編『実験化学講座　7　-電気物性，磁気物性-』（第5）丸善〈丸善〉、2004年。ISBN 4621073060。 

関連項目

• 四端子測定法
• 電気抵抗
• オームの法則
• 内部抵抗